Veröffentlicht von Inhaltsverzeichnis
📊 Seitenaufrufe: 335
MagnetiCalc berechnet auf interaktive, komfortable und performante Weise die statische magnetische Flussdichte, das Vektorpotential, die Energie, die Selbstinduktivität und das magnetische Dipolmoment beliebig geformter Spulen. In einer VisPy / OpenGL-beschleunigten PyQt5 GUI wird die statische magnetische Flussdichte (-Feld, in Tesla) oder das magnetische Vektorpotential (
-Feld, in Tesla-Meter) dreidimensional und interaktiv dargestellt; zum Hervorheben der Feldeigenschaften werden verschiedene Metriken verwendet.
Experimentelles Feature: Zur Berechnung der Energie und Selbstinduktivität permeabler (i.e. ferromagnetischer) Kernmedien können diese als Regionen variabler relativer Permeabilität modelliert werden; da die Kernsättigung momentan jedoch nicht modelliert wird, führt dies zu überhöhten Werten der Flussdichte.
Zur Beschleunigung der Feldberechnung verwendet MagnetiCalc Just-In-Time-Kompilierung (JIT) und, falls eine unterstützte Grafikkarte verfügbar ist, sogar GPU-Beschleunigung (CUDA).
Download
Der Quellcode und die Installationsanleitung finden sich im MagnetiCalc GitHub-Repository:
Funktionsweise
Die Feldberechnung wurde mithilfe des Biot-Savart-Gesetzes [1] implementiert und erlaubt die Verwendung mehrerer Prozessorkerne. Durch den Einsatz leicht zu parametrisierender Abtastvolumen (engl. sampling volume) lässt sich die Berechnung selektiv auf Gitter beliebiger Form und beliebiger Permeabilität beschränken (experimentell).
Die Form eines elektischen Leiters wird als dreidimensionale, stückweise stetige Kurve repräsentiert. Beliebige Leiterschleifen werden in differenzielle Leiterelemente (engl. slices) zerlegt, wovon jedes zum gesamten resultierenden Feld ( oder
) an einem festen Abtastpunkt beiträgt.
Die Feldstärke (oder der Feldwinkel in einer Ebene) wird an jedem Abtastpunkt durch Pfeile und/oder Kügelchen dargestellt, deren Farbe und Transparenz (Alpha-Wert) jeweils individuell durch eine der verfügbaren Metriken abgebildet werden.
[1]: Jackson, Klassische Elektrodynamik, 5. Auflage, S. 204, (5.4).Weitere Informationen und alle relevanten Formeln finden sich im MagnetiCalc GitHub-Repository.
Verifikation
Magnetische Flussdichte
Im Zentrum einer Leiterschleife von 1 cm Radius, durch die ein Strom von 1 A fließt, berechnet MagnetiCalc eine magnetische Flussdichte von 62,8 Mikrotesla. In einem axialen Abstand von 1 cm ist das B-Feld bereits auf 22,2 Mikrotesla abgefallen.
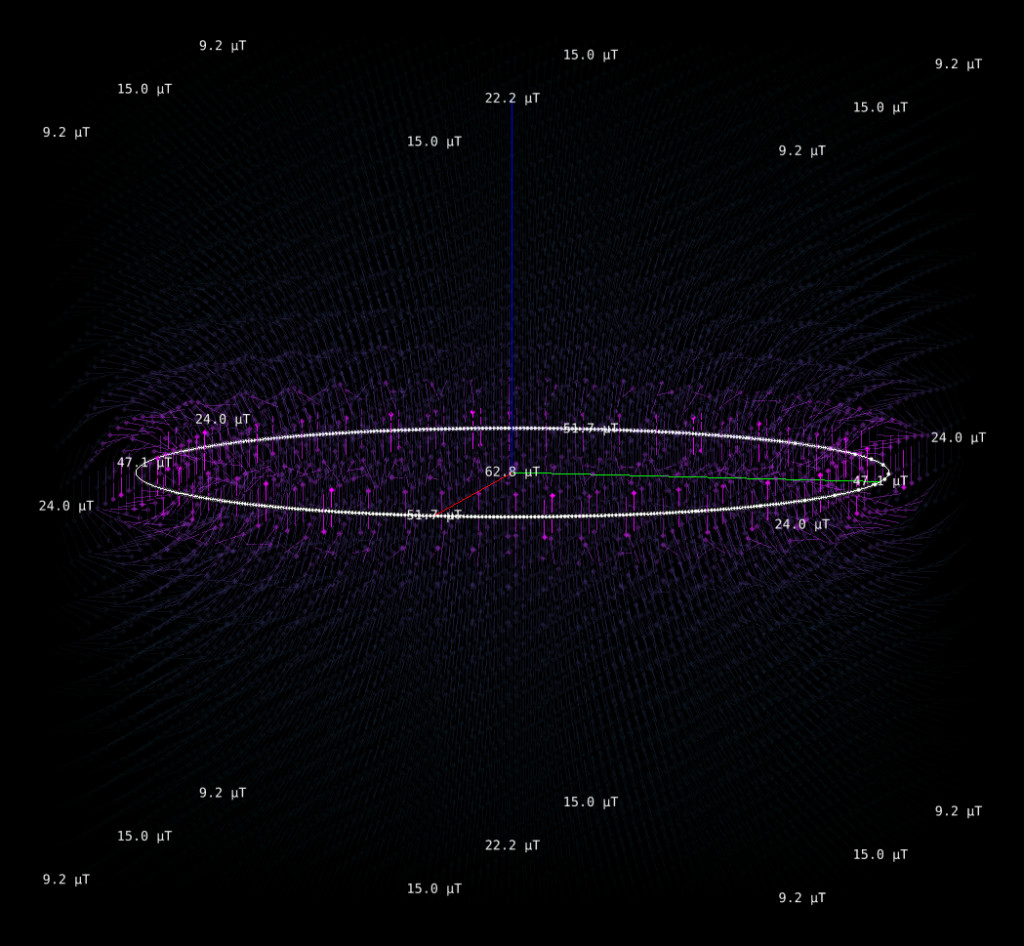
Dieses von MagnetiCalc berechnete Ergebnis deckt sich hervorragend mit der Theorie. Auf der HyperPhysics-Website gibt es einen simplen Online-Rechner für das Biot-Savart-Gesetz, dessen Ergebnisse exakt mit denen von MagnetiCalc übereinstimmen:
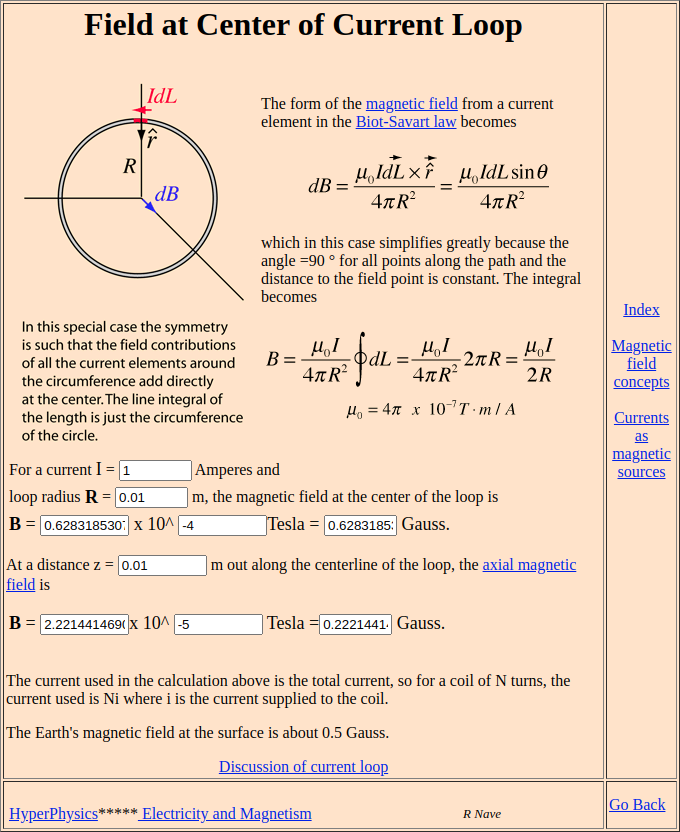
Selbstinduktivität
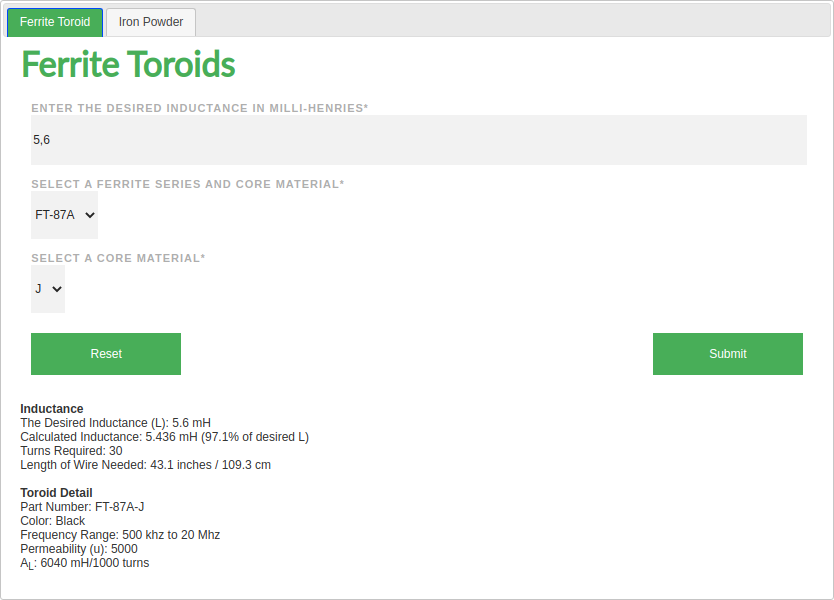
Als experimentelles Feature kann MagnetiCalc auch die Selbstinduktivität von permeablen (i.e. ferromagnetischen) Kernen berechnen. Für diesen Test habe ich mich an dem Ferrit-Ringkern
FT-87A-J
von Amidon [1] orientiert, welcher eine besonders hohe Anfangspermeabilität von µr = 5000 aufweist.
Die Geometrie und die relative Permeabilität des Kernmaterials kann durch Beschränkung des Abtastvolumens festgelegt werden; hierfür dient der Constraint Editor:
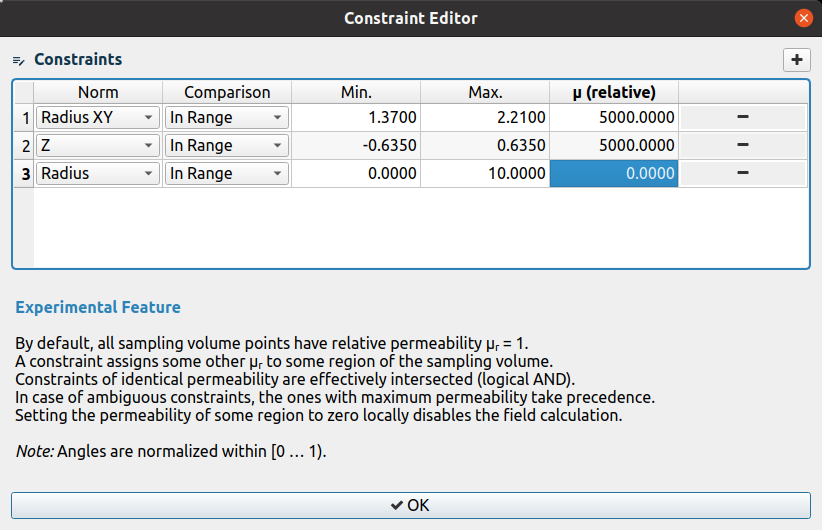
Bei 30 Windungen berechnet MagnetiCalc eine Selbstinduktivität von 5,6 mH:
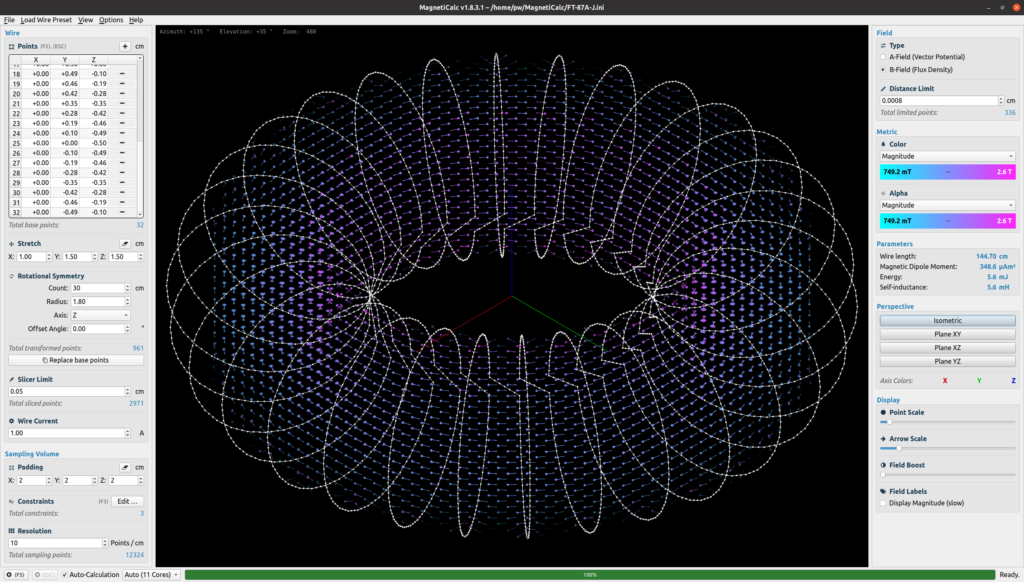
Der simple Online-Rechner Ham Calc liefert bei 30 Windungen mit einer Selbstinduktivität von 5,4 mH ein vergleichbares Ergebnis:
Videos
Galerie
Betrag des magnetischen Vektorpotentials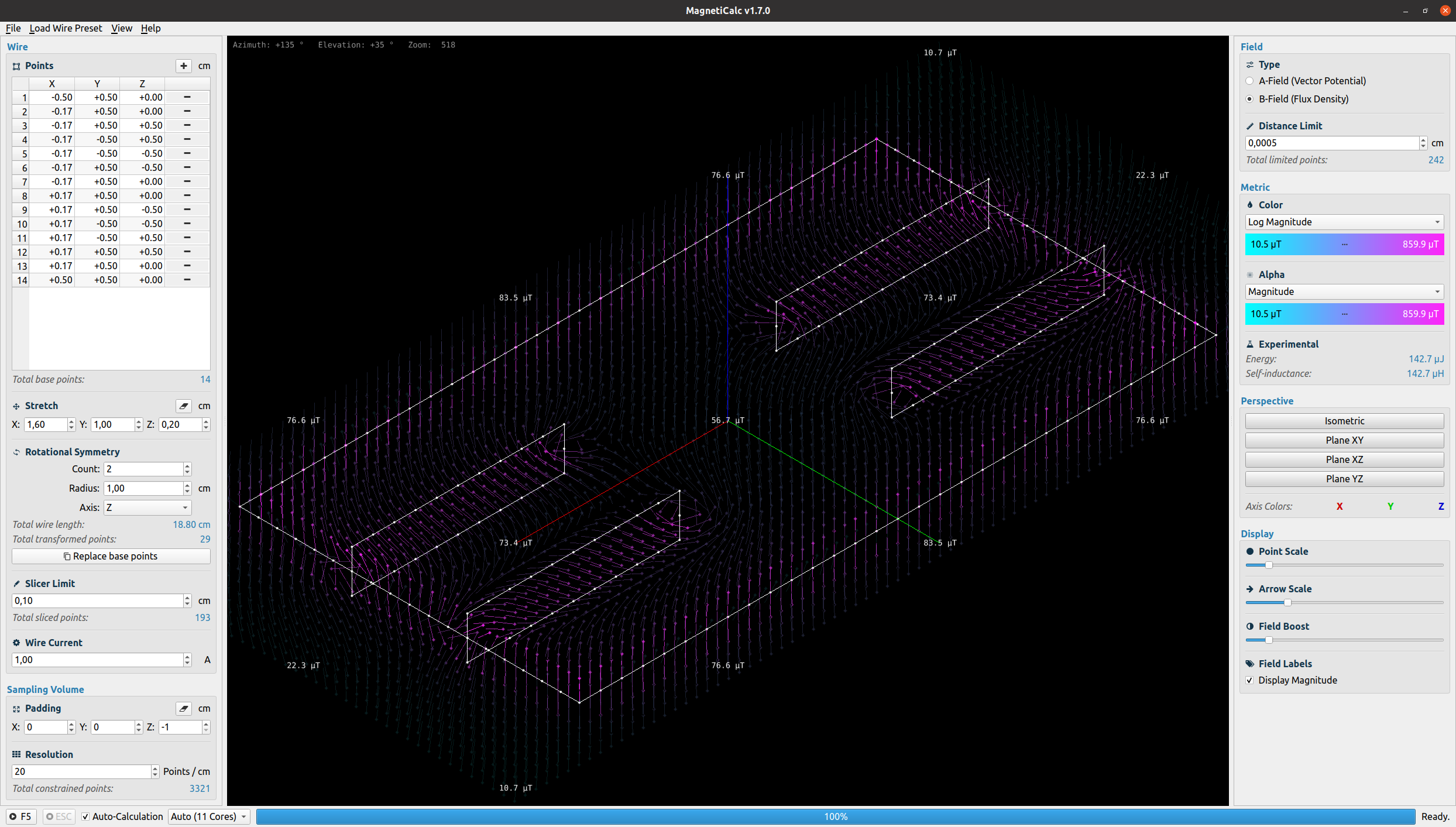 
Logarithmischer Betrag der magnetischen Flussdichte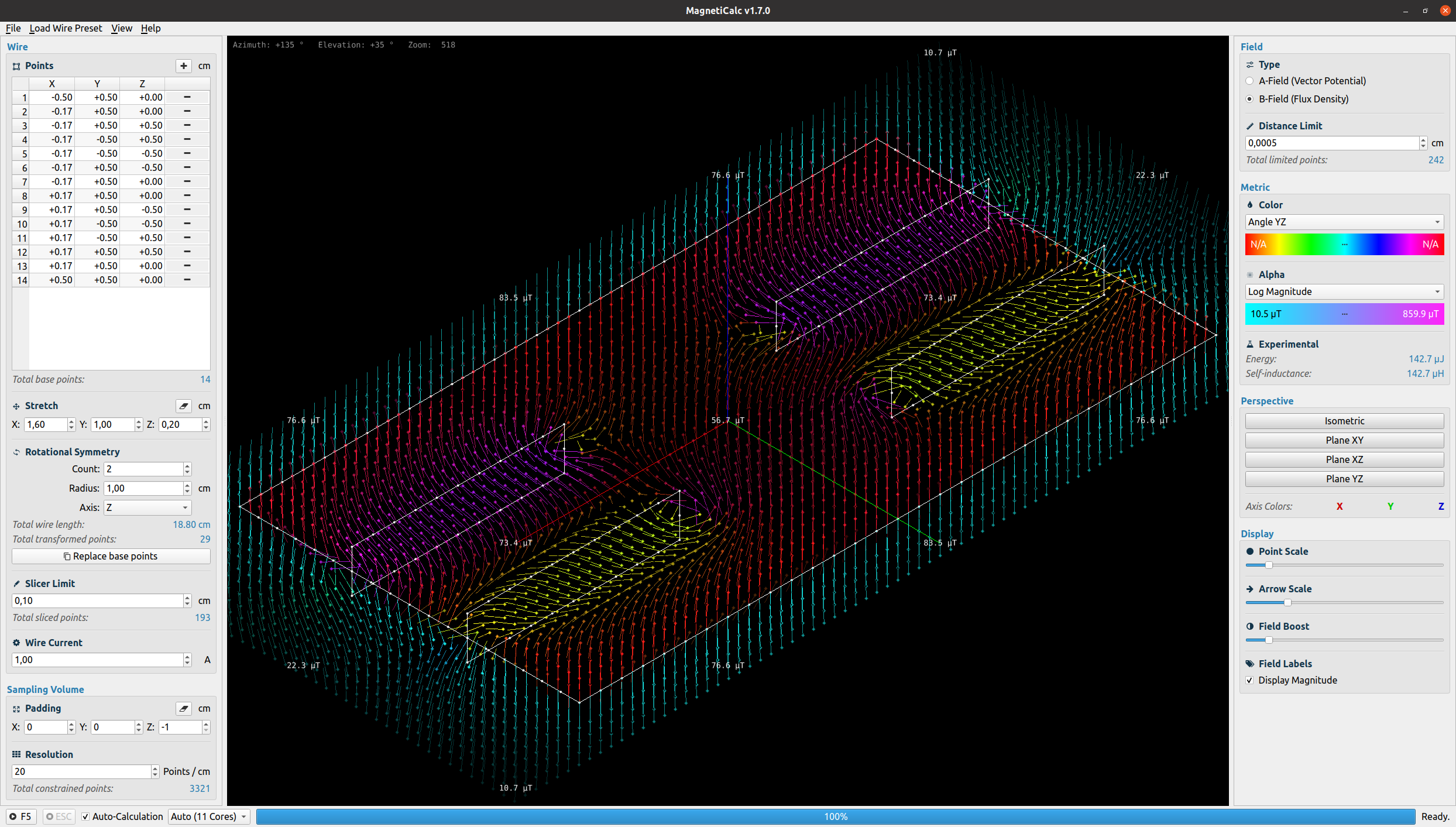 
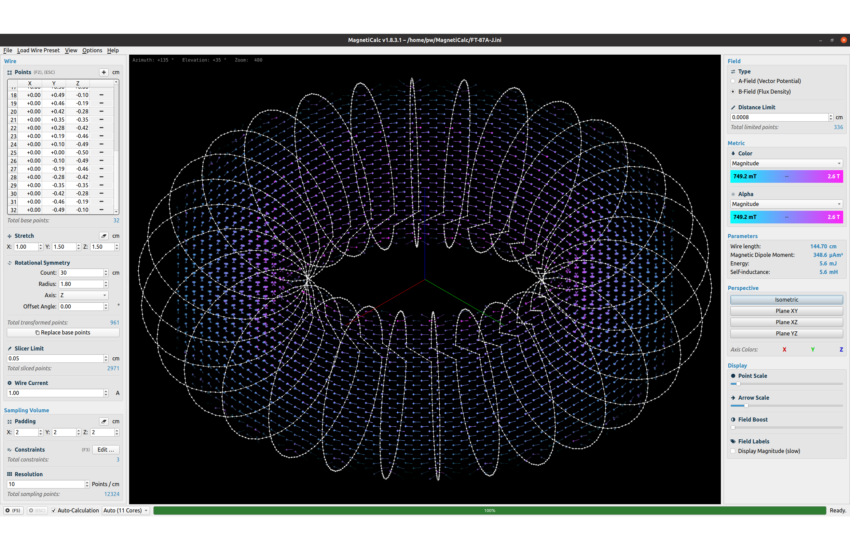
YZ-Winkel der magnetischen Flussdichte